Abstract

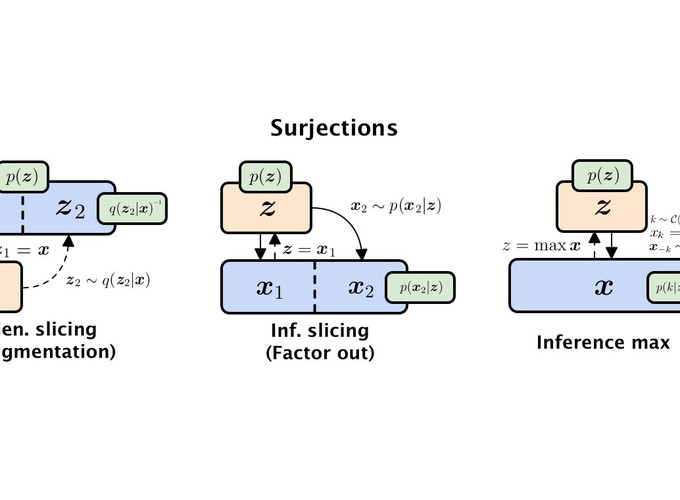
Normalizing flows and variational autoencoders are powerful generative models that can represent complicated density functions. However, they both impose constraints on the models: Normalizing flows use bijective transformations to model densities whereas VAEs learn stochastic transformations that are non-invertible and thus typically do not provide tractable estimates of the marginal likelihood. In this paper, we introduce SurVAE Flows: A modular framework of composable transformations that encompasses VAEs and normalizing flows. SurVAE Flows bridge the gap between normalizing flows and VAEs with surjective transformations, wherein the transformations are deterministic in one direction – thereby allowing exact likelihood computation, and stochastic in the reverse direction – hence providing a lower bound on the corresponding likelihood. We show that several recently proposed methods, including dequantization and augmented normalizing flows, can be expressed as SurVAE Flows. Finally, we introduce common operations such as the max value, the absolute value, sorting and stochastic permutation as composable layers in SurVAE Flows.