Abstract

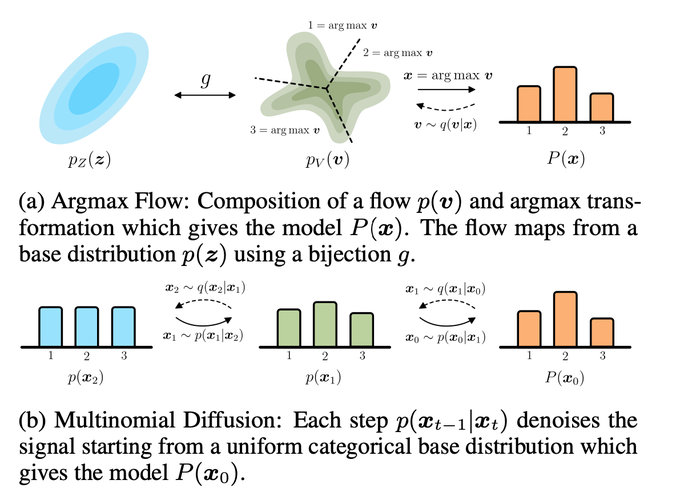
Generative flows and diffusion models have been predominantly trained on ordinal data, for example natural images. This paper introduces two extensions of flows and diffusion for categorical data such as language or image segmentation: Argmax Flows and Multinomial Diffusion. Argmax Flows are defined by a composition of a continuous distribution (such as a normalizing flow), and an argmax function. To optimize this model, we learn a probabilistic inverse for the argmax that lifts the categorical data to a continuous space. Multinomial Diffusion gradually adds categorical noise in a diffusion process, for which the generative denoising process is learned. We demonstrate that our method outperforms existing dequantization approaches on text modelling and modelling on image segmentation maps in log-likelihood.